Random walk approach

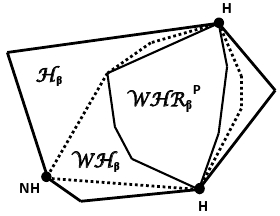
Exploiting a result due to Feinberg [6], we can constrain the set of discounted occupational measures (in a Mfarkov decision process induced by a given graph) by a single cut, and make a simple normalization to construct a polytope H_β that is nonempty whenever the graph is Hamiltonian and which – in a prescribed sense – contains all the Hamiltonian cycles among its extreme points. While the latter polytope has been exploited as a base for two successful heuristic algorithms (e.g. see [1], [5]), we have evidence that it may also reveal certain fundamental properties of Hamiltonian graphs, when the parameter β is sufficiently near 1.

In particular, we can construct two smaller polytopes WH_β and WH^p_β such that WH^p_β ⊂ WH_β ⊂ H_β and, more importantly, the only extreme points that WH^p_β and H_β have in common correspond precisely to Hamiltonian cycles. This is, schematically, portrayed in the figure below. Recently, Filar and Eshragh [4] designed a random walk, pivoting, algorithm on the extreme points of WH^p_β and H_β that in – numerical testing – found Hamiltonian cycles in 2 to 34 random pivots for randomly generated (sparse) graphs with number of vertices ranging from 20 to 150.

As expected, the above random walk algorithm will find a Hamiltonian cycle (if there is one) in finite time, with probability one (see [4]). However, what makes this idea exciting is that the observed slow growth of the number of random pivots in N (number of vertices) suggests that the following, much more powerful, result may also be true.

Conjecture: Let A be a suitably designed random walk algorithm and Y be the random variable denoting the number of extreme points that A will need to examine to identify a Hamiltonian cycle (if there is one). Then there exist polynomials q₁(log(β), N) and q₂(log(β), N) (with positive coefficients of the leading power of N) such that for β sufficiently near 1, the probability Pr(Y > q₁(log(β), N)) ≤ exp{-q₂(log(β), N)}.

These results were first derived in Eshragh’s PhD thesis [2] which was later published as [3].

PUBLICATIONS

[1] Ejov, V., Filar, J.A., Haythorpe, M. and Nguyen, G.T. “Refined MDP-based branch-and-fix algorithm for the Hamiltonian Cycle Problem.” Mathematics of Operations Research, 34(3):758-768, 2009. ACM Digital Library

[2] Eshragh, A. “Hamiltonian cycles and the space of discounted occupational measures.” University of South Australia, 2011. Trove

[3] Eshragh, A. “Hamiltonian Cycles and the Space of Discounted Occupational Measure.” Lambert Academic Publishers, Saarbrücken, 2011.

[4] Eshragh, A. and Filar, J.A. “Hamiltonian Cycles, Random Walks, and Discounted Occupational Measures.” Mathematics of Operations Research, 36(2):258-270, 2011. Informs Online

[5] Eshragh, A., Filar, J.A. and Haythorpe, M. “A hybrid simulation-optimization algorithm for the Hamiltonian cycle problem.” Annals of Operations Research, 189(1):103-125, 2011. SpringerLink

[6] Feinberg, E. “Constrained discounted Markov decision processes and Hamiltonian cycles.” Mathematics of Operations Research, 25(1):130-140, 2000. JSTOR