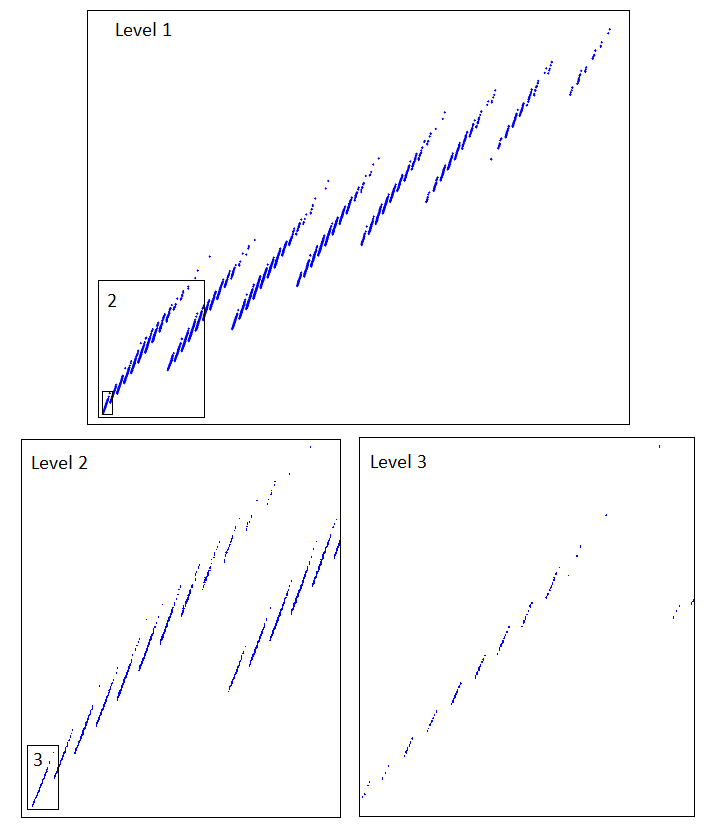
Fractal-like structure of cubic graphs
One benefit of investigating a difficult problem such as the HCP is that these investigations lead to deeper understanding of related phenomena that may have intrinsic interest in their own right. Hence it is not surprising that the Flinders Hamiltonian Cycle Project has had some spin-offs that are, perhaps, worthy of an explicit mention.
The most natural of these is related to the relationship of a graph G with the spectra of matrices that contain all the pertinent information about that graph. In particular, recall that the adjacency matrix A of an N node graph is simply the N × N matrix with 1’s in all ij-entries that correspond to arcs (i, j) present in G and with 0’s in all other entries.
It is clear that A contains all the information about the graph G and since the spectrum of a matrix contains a lot of essential information about that matrix, it is natural to ask whether it is possible to differentiate between Hamiltonian and non-Hamiltonian graphs on the basis of the spectra of their respective adjacency matrices?
Regrettably, the answer to the above question is negative. For instance, in Filar et al [3] an example is given of two, cubic, connected, co-spectral graphs where one is Hamiltonian and the other is not. Nonetheless, a deeper analysis of the spectra reveals an interesting classification of the whole family of cubic graphs.
Consider a cubic graph of size N, and its adjacency matrix A. Then 1/3A is a real, symmetric, stochastic matrix whose eigenvalues therefore lie between -1 and 1. We can take the exponential of each of the eigenvalues, and find the mean and variance of these exponentiated eigenvalues. This gives us a 2-dimensional co-ordinate for a cubic graph. We can produce a set of co-ordinates for each cubic graph of size N and plot them all on the same figure. The resulting graph displays the following thread-like, multifilar, structure.