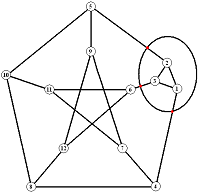
Named after Sir William Hamilton’s investigations of the dodecahedral graph in 1857, the Hamiltonian cycle problem (HCP, for short) is a classical graph theory problem that can be summarised thus:
Given a graph containing N vertices determine whether it contains a simple cycle of length N.
Such a cycle is called a Hamiltonian cycle. The HCP has become a challenge that attracts mathematical minds both in its own right and because of its close relationship to the famous Travelling salesman problem (TSP), that calls for the identification of a Hamiltonian cycle with the lowest cost possible in a graph where every edge has a known cost associated with “travelling” along that edge. An efficient solution of the TSP would have an enormous impact in operations research, optimisation and computer science. However, from a mathematical perspective the underlying difficulty of the TSP is, perhaps, hidden in the Hamiltonian cycle problem. Hence, we focus on the latter.
The FHCP is a team project that aims to exploit novel stochastic and deterministic techniques to (i) explain the underlying theoretical difficulty of the HCP, (ii) characterise classes of graphs that are particularly hard to solve and (iii) produce world-class algorithms that enable the efficient solution of most instance of the problem on graphs not exceeding 5000 vertices.
Based at Flinders University, South Australia, FHCP is led by Jerzy Filar and Vladimir Ejov. The team includes Flinders University students, research fellows and eminent national and international collaborators. FHCP team members have developed numerous approaches to analysing and solving the Hamiltonian cycle problem. A summary of these approaches is given below, with the most recent ideas listed first. For more detail, visit the respective project pages.
Visualisation of a solution to Euler’s Knight’s Tour Problem.