Genetic theory of cubic graphs
The genetic theory of cubic graphs is an approach to classification of cubic graphs that involves tracking down the characteristics of a given graph by means of smaller graphs using graph decomposition. Namely, a graph is a descendant of some smaller ancestor graphs and the characteristics of the descendant graph are inherited from the genetics of the ancestor graphs. Such an approach to graph theory is especially motivated by problems such as the Hamiltonian Cycle Problem (HCP, for short) where the difficulty of the problem increases rapidly with the size of the graph. Additionally, this approach could potentially be useful in determining other important characteristics of cubic graphs such as planarity.
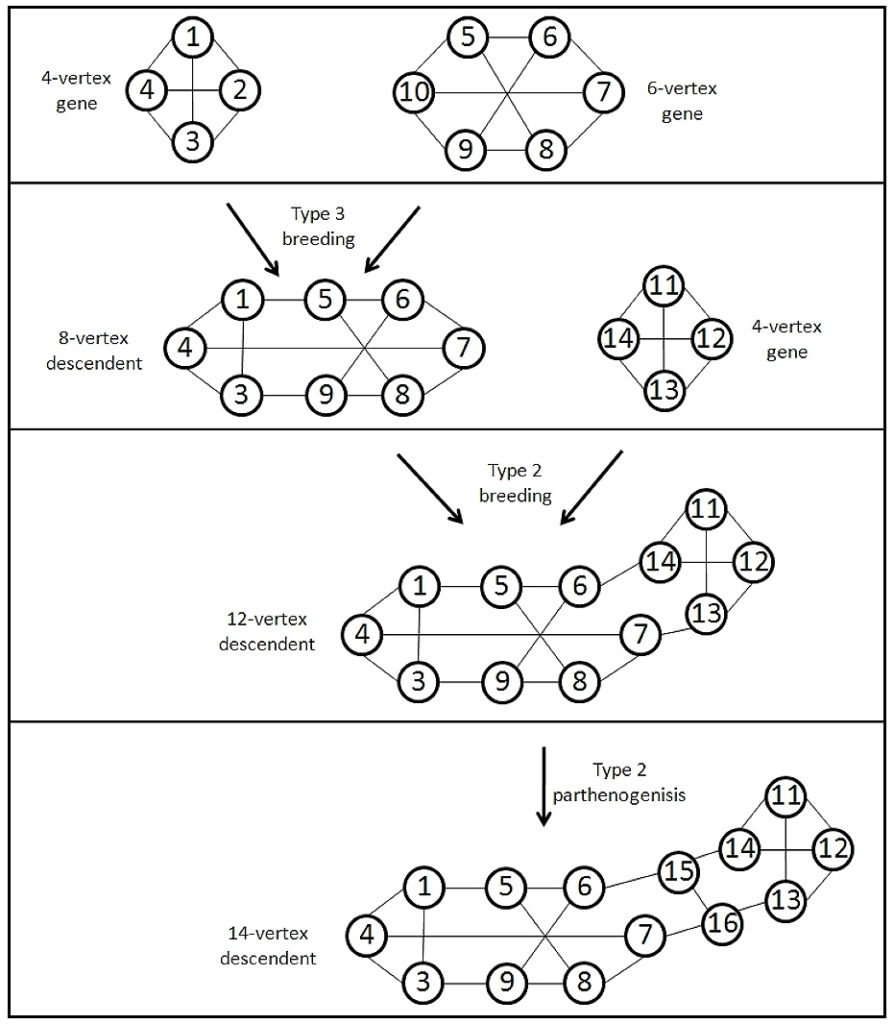
Consider a cutset in a graph that contains only non-adjacent edges, such that no proper subset of this cutset is also a cutset. We call such a cutset, of cardinality k, a k-cracker, and when k is no larger than 3 we call it a cubic cracker. We propose a partitioning of the set of unlabelled, connected, cubic graphs into two disjoint subsets, namely descendants and genes. The distinguishing feature is that descendants contain at least one cubic cracker, whereas genes contain no cubic crackers. Descendants are much more common than genes.
The names descendant and gene are selected because Baniasadi et al [1] prove that every descendant can be constructed from a finite set of genes through the use of six breeding operations. Such a set of genes is called a complete family of ancestor genes for the descendant. In such a way the authors of [1] demonstrate that graphs can be viewed as offsprings of their ancestors, illustrated by an ancestral family tree such as the following: